预估比例

这章主要讲如何选择 prior distributions。

import numpy as np 
from empiricaldist import Pmf 
import matplotlib.pyplot as plt 
import pandas as pd
from scipy.stats import binom 

一枚硬币，随机抛掷 250 次，观测的结果是 140 次正面朝上，110 次背面朝上。将这枚硬币随机抛掷一次，是正面朝上的概率最有可能是多少？

上图来自搜狐

我们可以用「分布」那部分的例子来思考。我们可以把这个问题转化为：

我们目前有 \(n\) 枚硬币，其各有如下特征：

• 随机抛硬币 0，正面朝上的概率是 0/n

• 随机抛硬币 1，正面朝上的概率是 1/n

• 随机抛硬币 2，正面朝上的概率是 2/n
  …

• 随机抛硬币 n，正面朝上的概率是 n/n

我们从这些硬币中随机挑了一枚，随机抛掷 250 次，观测的结果是 140 次正面朝上，110 次背面朝上。这枚硬币最有可能是哪枚硬币？

我们先用 uniform prior，也就是说，每一枚硬币是该硬币的概率相同。

# 稍微修改一下之前的 update_bowls_pmf
def update_coins_pmf(n, h, t):
    """
    n: 总共几枚硬币
    h: 正面朝上
    t: 背面朝上
    """
    hypos = np.linspace(0, 1, n+1)
    prior = Pmf(1, hypos)
    likelihood_head = [i/(n-1) for i in range(n+1)]
    likelihood_tail = [1- i for i in likelihood_head]
    likelihood = {
        "head": likelihood_head,
        "tail": likelihood_tail
    }
    dataset = ["head"]*h + ["tail"]*t
    posterior = prior.copy()
    for data in dataset:
        posterior *= likelihood[data]
    posterior.normalize()
    return posterior

hypos = np.linspace(0, 1, 10)
hypos

array([0.        , 0.11111111, 0.22222222, 0.33333333, 0.44444444,
       0.55555556, 0.66666667, 0.77777778, 0.88888889, 1.        ])

prior = Pmf(1, hypos)
prior

	probs
0.000000	1
0.111111	1
0.222222	1
0.333333	1
0.444444	1
0.555556	1
0.666667	1
0.777778	1
0.888889	1
1.000000	1

posterior = update_coins_pmf(1000, 140, 110)
df = pd.DataFrame(posterior, columns=['probs'])
df = df.reset_index(names = "proportion of heads (x)")
df.plot.scatter(x = "proportion of heads (x)", y="probs", 
                s = 4,
                label = "140 heads out of 250")
# posterior.plot(label="posterior", color="steelblue")
# plt.xlabel("Proportion of heads (x)")
plt.ylabel("Probability mass function")
plt.legend()
plt.title("Posterior distribution of x")
plt.show()

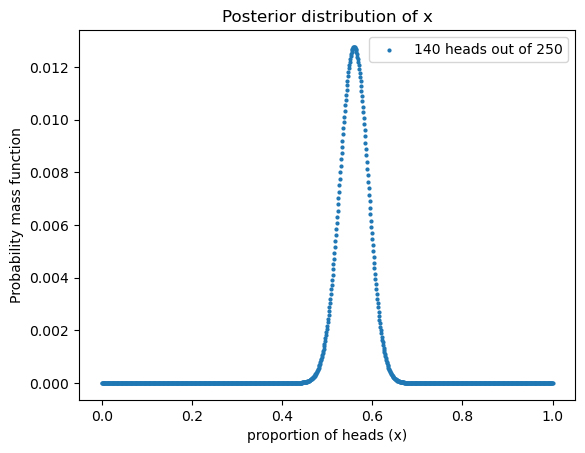
上面我们用到的是 uniform prior：

hypos = np.linspace(0, 1, 1001)
uniform = Pmf(1, hypos, name = "uniform")
uniform.normalize()
df = pd.DataFrame(uniform)
df = df.reset_index(names = "proportion of heads (x)")
df.plot.scatter(x = "proportion of heads (x)", y="uniform", s= 4)
# uniform.plot(label="proportion of heads (x)", color="steelblue")
plt.xlabel("Proportion of heads (x)")
plt.ylabel("Probability mass function")
plt.title("Uniform prior")
plt.show()

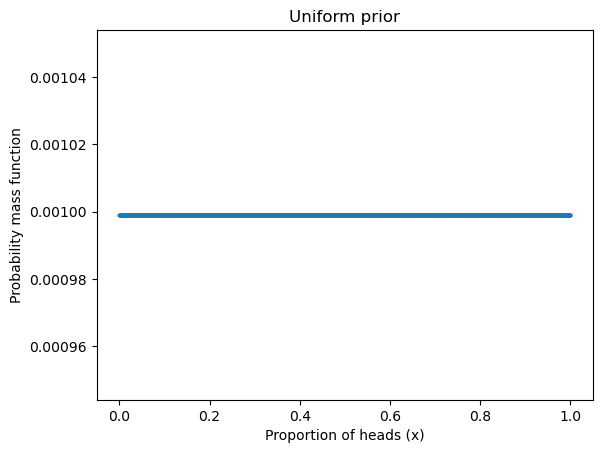
但是该 prior 并不一定是 uniform 的，也可能是这样子：

hypos = np.linspace(0, 1, 1001)
ramp_up = np.arange(500)
ramp_down = np.arange(500, -1, -1)
a = np.append(ramp_up, ramp_down)
triangle = Pmf(a, hypos, name = "triangle")
triangle.normalize()
df = pd.DataFrame(triangle)
df = df.reset_index(names = "proportion of heads (x)")
df.plot.scatter(
    x = "proportion of heads (x)", 
    y="triangle", 
    color = "orange",
    s = 4
    )
# triangle.plot(label="proportion of heads (x)", color="steelblue")
plt.xlabel("Proportion of heads (x)")
plt.ylabel("Probability mass function")
plt.title("Triangle prior")
plt.show()

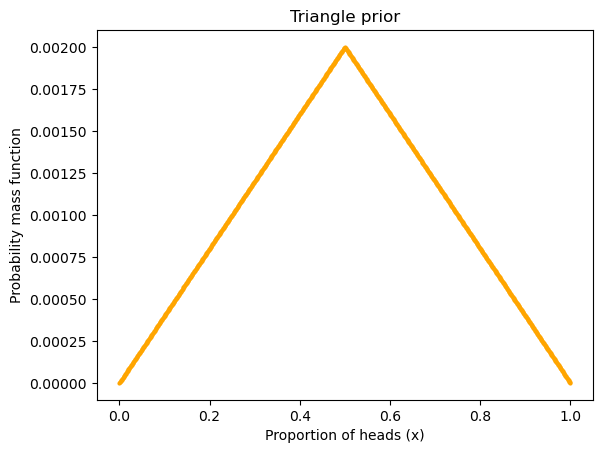
如果我们用如此的 prior，结果是什么呢：

# 稍微修改一下之前的 update_coins_pmf 以便可以修改 prior 
def update_coins_pmf(n, h, t):
    """
    n: 总共几枚硬币
    h: 正面朝上
    t: 背面朝上
    """
    hypos = np.linspace(0, 1, n+1)
    ramp_up = np.arange(n/2)
    ramp_down = np.arange(n/2, -1, -1)
    a = np.append(ramp_up, ramp_down)
    prior = Pmf(a, hypos, name = "triangle")
    likelihood_head = [i/(n-1) for i in range(n+1)]
    likelihood_tail = [1- i for i in likelihood_head]
    likelihood = {
        "head": likelihood_head,
        "tail": likelihood_tail
    }
    dataset = ["head"]*h + ["tail"]*t
    posterior = prior.copy()
    for data in dataset:
        posterior *= likelihood[data]
    posterior.normalize()
    return posterior

posterior = update_coins_pmf(n = 1000, h = 140, t = 110)
df = pd.DataFrame(posterior)
df = df.reset_index(names = "proportion of heads (x)")
df.plot.scatter(
    x = "proportion of heads (x)", 
    y="triangle", 
    label = "140 heads out of 250",
    color = "orange",
    s= 4
    )
# posterior.plot(label="posterior", color="steelblue")
# plt.xlabel("Proportion of heads (x)")
plt.ylabel("Probability mass function")
plt.legend()
plt.title("Posterior distribution of x")
plt.show()

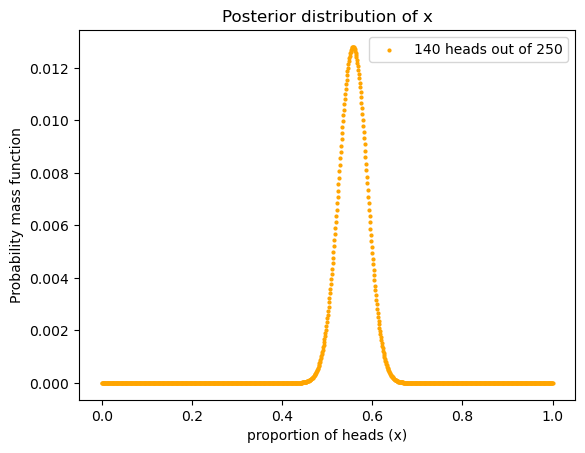
我们看到和用 uniform prior 结果差不多。这说明什么？这说明数据够多的话，prior 对 posterior 的影响没那么大。

Batch updating

上面我们是一个数据点一个数据点地在更新 posterior：

for data in dataset:
    posterior *= likelihood[data]

我们能不能直接得到一串的 likelihood，这样两个向量逐元素想乘以 (element-wise multiplication) 就可以了？我们需要用到 binomial distribution 公式：

\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]

我们用 scipy.stats.binom。

scipy.stats.binom.pmf(k, n, p)

其中 k 是正面朝上的次数，n 是总攻抛掷的次数， p 是正面朝上的概率。需要注意的是，p 可以是一个数，也可以是一组数。当 p 是一个数时，其结果是一个数。当 p 是一组数时，结果是一组数。

def update_binom(heads, tosses, prior):
    """
    heads: number of heads 
    tosses: total tosses 
    prior: prior distribution; should be a empiricaldist.pmf object (a Series)
    """
    # 0/n, 1/n, 2/n ...
    coin_head_probabilities = prior.qs
    likelihood = binom.pmf(k = heads, n = tosses, p = coin_head_probabilities)
    posterior = prior.copy()
    posterior *= likelihood 
    posterior.normalize()
    return posterior

# n: number of coins
n = 1001
tosses = 250
# number of heads out of 250 tosses
heads = 140
hypos = np.linspace(0, 1, n)
uniform2 = Pmf(1, hypos, name = "uniform2")
posterior = update_binom(heads, tosses, uniform2)
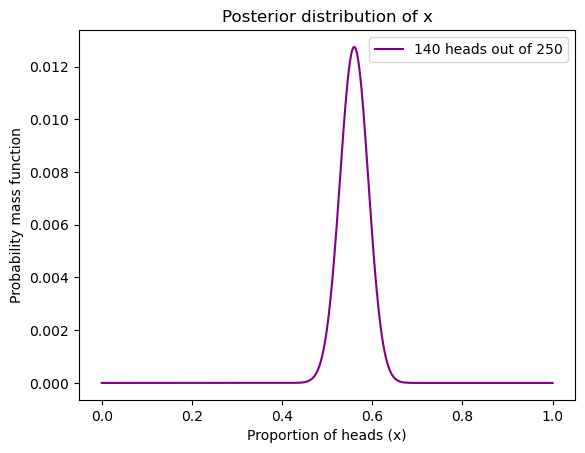
posterior.plot(label = "140 heads out of 250", color="purple")
plt.legend()
plt.xlabel("Proportion of heads (x)")
plt.ylabel("Probability mass function")
plt.title("Posterior distribution of x")
# 这里为了简单，我把 discrete distribution 画成了 continuous 的，希望不会造成读者误解。
# 其实，当 n 无限大时，最终的结果就是下面这样

Text(0.5, 1.0, 'Posterior distribution of x')